La fission de noyaux atomiques est un processus complexe qui nécessite de bien connaître la structure du noyau fissionnant. L’étude de ce phénomène est donc un sacré périple qui implique de s’aventurer dans l’espace des déformations du noyau. Ici, nous allons faire une visite guidée des hypersurfaces que l’on peut y trouver et allons voir comment elles ont été obtenues. Nous irons doucement, l’objectif est de s’amuser.
Si vous cherchez un coin sympa pour passer vos vacances, oubliez les destinations clichées et vivez plutôt des aventures inoubliables en famille en explorant les chaînes de montagnes de Fission, la nouvelle région française située en plein Massif Central et qui s’est affranchie des autres régions alentours.
Comme tout bon guide touristique, il me faut vous conter son histoire. En 1911, Rutherford découvre que l’atome est composé d’une région centrale quasi-ponctuelle et de charge positive (le noyau), entourée d’électrons de sorte que l’ensemble est électriquement neutre.
Depuis cette découverte, la connaissance de la composition du noyau a progressé. On sait que le noyau est composé de deux types de particules : les protons et les neutrons, eux-mêmes composés de quarks. On sait également que ces quarks interagissent entre eux au moyen de l’interaction forte.
Pour obtenir ces informations, il a fallu "zoomer" toujours plus sur la matière. Pour fixer les idées, disons que l’extension spatiale de l’atome est ~10-10 m, celle du noyau ~10-15 m et celle des quarks 10-18 m. Il existe une certaine dualité entre extension spatiale et énergie d’une particule : plus on zoome sur la matière, plus on doit monter haut en énergie pour cela (c’est ce que font les accélérateurs de particules). Ainsi, la description des quarks se fait à haute énergie, on dispose en
effet d’une théorie incroyable pour décrire l’interaction forte dans ce domaine en énergie : la Chromodynamique Quantique (QCD en anglais).
Cependant, les choses se gâtent, la QCD aime efficacement rester dans sa zone de confort : les hautes énergies, elle ne parvient pas à décrire les objets qui vivent dans un régime plus faible, tels que les noyaux ou même ne serait-ce que les protons et neutrons. Cela n’a pas suffi à décourager les théoriciens, qui ont négocié avec QCD et sont arrivés à un compromis : la théorie effective chirale (χ-EFT en anglais), qui parvient à décrire les noyaux composés d’un faible nombre de protons ou neutrons (moins d’une dizaine).
Pour des noyaux plus lourds voire même très lourds (donc instables et capables de fissionner : 239Pu, 235U, 233U par exemple, utilisés dans l’industrie et la dissuasion nucléaires), on pourra se tourner vers des méthodes de mécanique quantique (relativiste ou non, les deux existent) inspirées de la chimie quantique et de la matière condensée : les méthodes de champ moyen.
Il faut savoir que l’étude du noyau atomique entre dans la catégorie des problèmes à N corps quantiques en interaction. Comme tout système quantique, l’évolution temporelle de ce système est régie par l’équation de Schrödinger mais, dans le cas présent, l’équation ne peut pas être résolue de manière exacte (même numériquement), c’est peu dire sur la complexité du problème. La première étape, et non des moindres, consiste à résoudre l’équation de Schrödinger indépendante du temps, qui ne peut pas non plus être résolue de manière exacte. C’est en cherchant des méthodes de résolution approchées que l’on arrive à notre théorie de champ moyen.
En effet, on peut simplifier considérablement le problème en considérant que les nucléons n’interagissent plus entre eux mais sont à la place plongés dans un potentiel, obtenu en moyennant les interactions au sein du noyau, qui les lie entre eux : le champ moyen. Cette approximation nous permet de passer d’une équation à N corps insoluble à un système de N équations à 1 corps qui, même si cela reste complexe, peut être résolu numériquement. Plus précisément, le champ moyen que l’on vient d’introduire est, au départ, choisi pour être un potentiel réaliste mais sans plus. Ce que l’on cherche à faire est de l’optimiser pour qu’il convienne en tout point au système étudié. Optimiser le champ moyen signifier minimiser l’énergie de liaison du noyau tout en imposant l’image de particules indépendantes, ce qui se fait au prix de la brisure possible de symétries qui auraient été présentes s’il avait été possible de décrire le noyau de manière exacte. Parmi les symétries brisées, se trouvent les symétries de nombre de neutrons et protons dans le noyau et la symétrie de rotation dans l’espace.
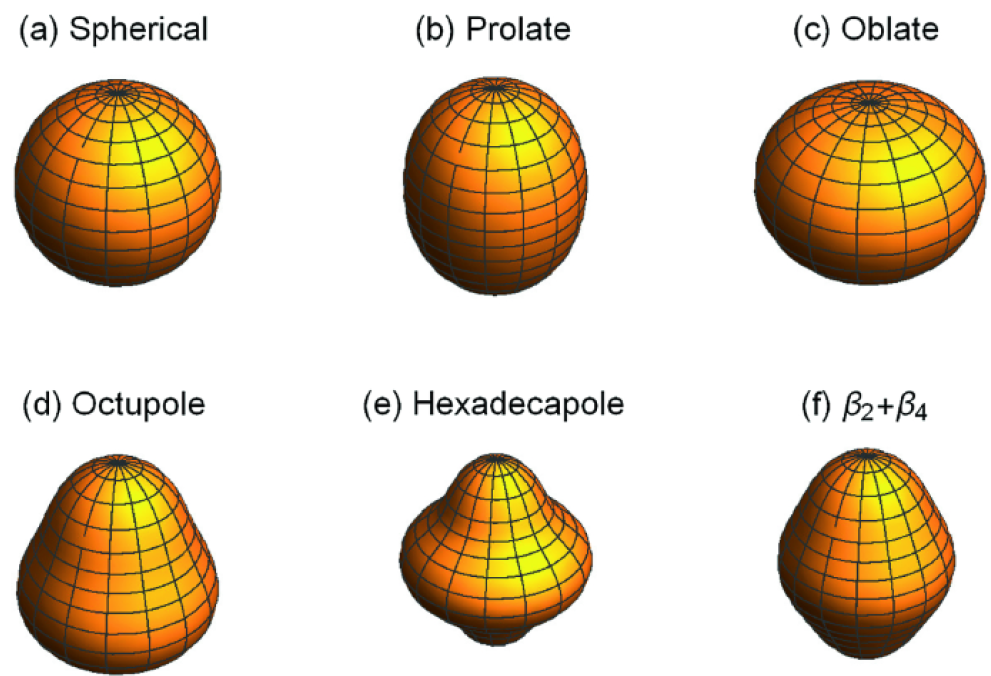
En brisant cette dernière symétrie, le noyau est décrit de manière approximative par un état qui le fait apparaître comme étant déformé. La déformation du noyau peut alors être vue comme une combinaison de déformations "élémentaires", dites multipolaires (Fig. 1 : Formes du noyau selon le moment multipolaire [1]). Par exemple, la déformation quadrupolaire est associée à un étirement (prolate) ou une compression (oblate) du noyau, c’est en l’étirant que l’on arrive à un seuil où le noyau se scinde en plusieurs fragments (souvent deux) : la scission. De même, lorsque le noyau est suffisamment étiré, il se peut qu’il laisse apparaître des préfragments de taille et masse inégales, il se scindera alors en noyaux pouvant appartenir à des régions de masse totalement différentes, cela est la trace des déformations octupolaires. Heureusement pour nous, il est possible de contraindre la déformation du noyau, transformant l’optimisation du champ moyen en un processus d’optimisation sous contraintes.
Revenons à nos montagnes et allons nous dégourdir les jambes !
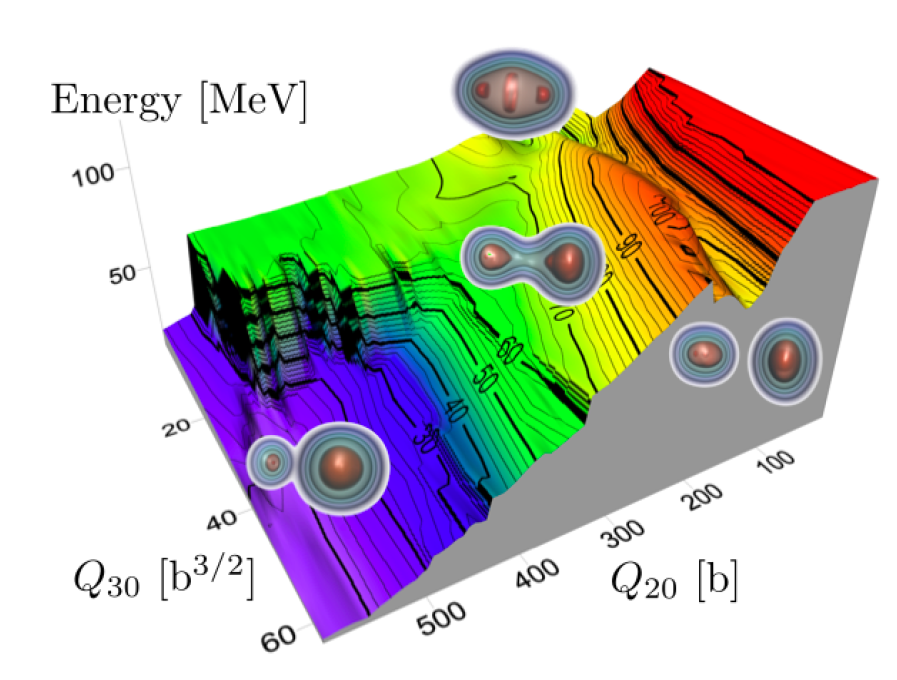
Il est possible de calculer l’énergie du noyau en fonction des différentes déformations multipolaires. L’hypersurface correspondante est appelée surface d’énergie potentielle (PES) (Fig. 2 : PES du 240Pu en fonction des moments quadrupolaire (Q20) et octupolaire (Q30) [2]). Étant donné un ensemble de contraintes sur la déformation du noyau, on cherche à trouver l’énergie la plus basse possible, on peut donc se promener dans la PES à la recherche du minimum correspondant. Cela peut se faire en utilisant la méthode du gradient.
L’idée est la suivante : suivre le gradient d’une fonction nous amène vers les valeurs maximales de la fonction, alors que suivre l’opposé du gradient nous amène vers ses valeurs minimales. Nous voilà munis d’une boussole très efficace, son seul inconvénient est sa sensibilité au point de départ. En effet, imaginons une surface possédant plusieurs minima locaux et un minimum global. Si le point de départ n’est pas bien choisi, suivre la direction du gradient risque de nous amener au mauvais minimum. De même, la méthode du gradient étant un processus itératif, il conviendra de souvent jeter un oeil à la direction indiquée par notre boussole (petit pas de gradient), pour ne pas se perdre.
Voici pour la petite histoire de cette charmante région. Maintenant que nous savons nous repérer dans ces contrées, allons escalader les barrières de Fission (maxima locaux des PES), faire de la randonnée sur les chemins de Fission (chemin de moindre énergie dans une PES jusqu’au point de scission) ou encore tenter de cartographier le paysage (photos multidimensionnelles interdites, cela serait trop simple).
References
[1] V.K.B Kota, SU(3) Symmetry in Atomic Nuclei, Springer, Singapore (2020)
https://doi.org/10.1007/978-981-15-3603-8_1.
[2] N. Schunck, D. Regnier, Theory of Nuclear Fission, Progress in Particle
and Nuclear Physics, LLNL-JRNL-830603 (2022).


