La lumière est un des éléments physiques que l’on côtoie le plus au quotidien, pourtant il y a beaucoup d’incompréhension sur ce qu’elle est et comment elle fonctionne. Par exemple peu de personnes savent que c’est une onde électromagnétique, et encore moins de personne savent comment fonctionne une onde électromagnétique. On va donc voir ce qu’est la lumière d’un point de vue électromagnétique, ensuite on va voir un exemple qui permet de comprendre comment fonctionne les impulsions lumineuses au niveau du champ électrique, de l’éclairement et la relation avec sa fréquence/période (Transformée de
Fourier).
Onde électromagnétique
Une onde électromagnétique est composée d’un champ électrique et magnétique qui se propagent
dans la même direction perpendiculairement l’un à l’autre (Fig.1).
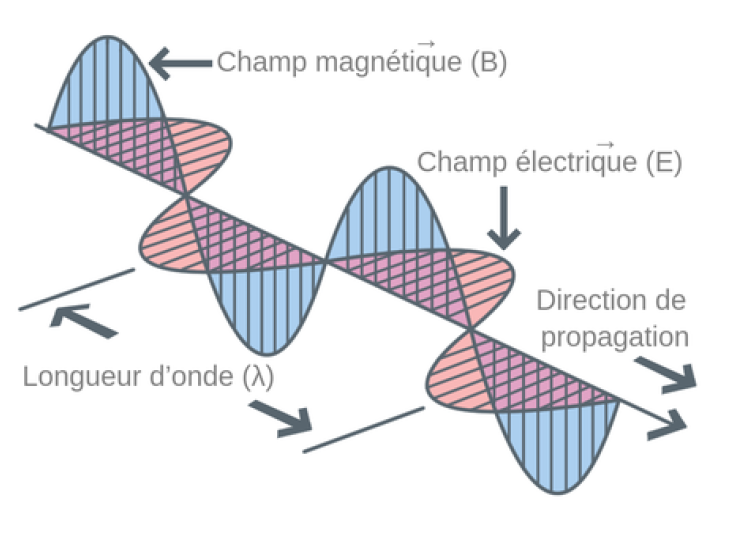
Figure 1 : Schéma d’une onde électromagnétique. En rouge le champ électrique et en bleu le
champ magnétique. La période spatiale (ou longueur d’onde) est l’écart entre deux maxima du
champ électrique. [1]
Ici on va se concentrer que sur la partie électrique, la période spatiale de ce champ (l’écart
entre deux maxima d’intensité en mètre, aussi appelé longueur d’onde) est relié à son énergie et à
sa fréquence :
Avec \(E\) l’énergie du champ (J), \(h\) la constante de Plank (J.s), \(c\) la vitesse de la lumière dans le vide (m/s), \(\lambda\) la période spatiale ou longueur d’onde (m), \(\nu\) la fréquence du champ (Hz), \(t\) le temps (s), et \(E(t)\) le champ électrique de l’onde (V/m) à ne pas confondre avec l’énergie.
La période de l’onde est reliée à sa couleur, une période de 400 nanomètre \((10^{−9}\) mètre) on voit du bleu/violet, 520 nm on voit du vert, 650 nm on voit du rouge par exemple. Nos yeux sont des détecteurs d’onde électromagn´etique qui captent les champ entre 400 et 800 nm environ ce qui nous permet de voir notre environnement en couleur, les périodes en dessous de 400 nm correspondent aux ultra-violet, rayon X etc... Et les périodes au dessus correspondent au infra-rouge micro-onde, onde radio etc...
Un élément que l’on remarque est que ce champ oscille et pourtant au quotidien on voit juste un flux continue de lumière. Cette remarque nous permet d’introduire une autre grandeur importante qui est l’éclairement \(I(t)\) (W/cm\(^{2}\)), en effet le temps de réponse de l’oeil humain est autour de la milliseconde (\(10^{−3}\) seconde) et l’électronique au minimum vers la nanoseconde (\(10^{−9}\) seconde). Cependant, la période d’oscillation du champ électrique est autour de la femtoseconde (\(10^{-15}\) seconde), soit le temps de faire un millier de milliard d’oscillation le temps que nos yeux ne comprennent qu’une seule information. On observe donc qu’une moyenne du signal qui est le module au carré du champ appelé éclairement.
Effet de modulation de la lumière
On vient de voir ce qu’était un champ électrique continu, mais qu’est ce qu’il lui arrive si par
exemple il est coupé spatialement à intervale régulier (Fig.2) :
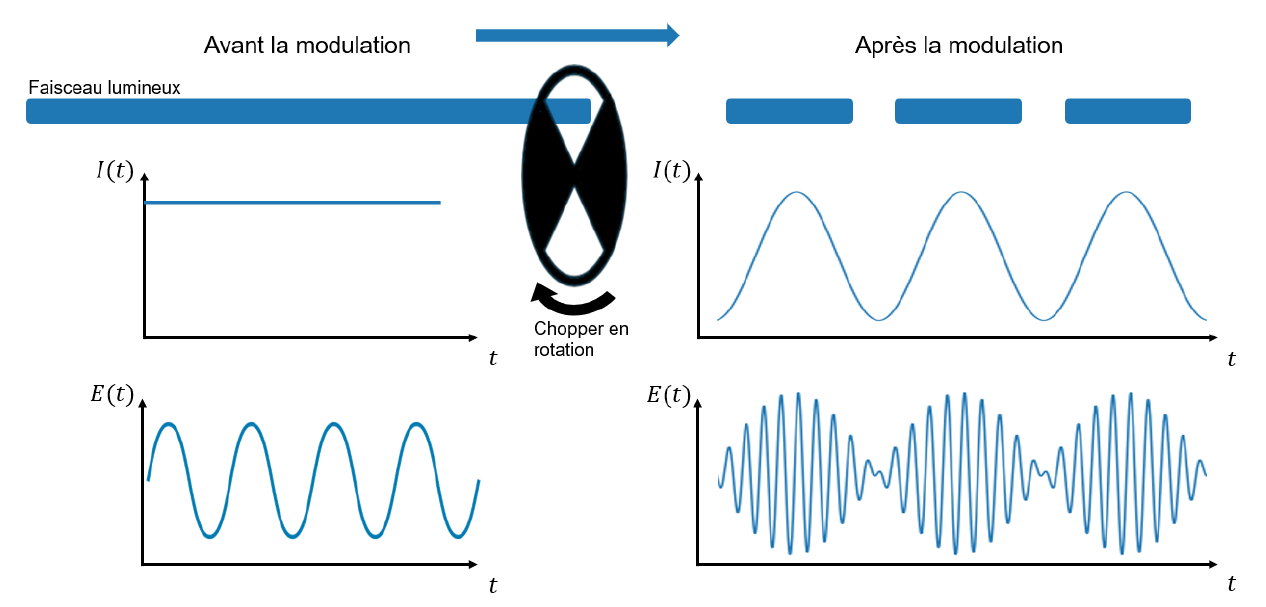
Figure 2 : Schéma de découpe spatiale d’un faisceau lumineux par un chopper. Le chopper va
créer des zones avec du signal et d’autre sans, ce qui va moduler l’intensité du signal dans le temps
et donc aussi modifier son champ électrique.
Sur la figure 2, on constate donc que notre éclairement \(I(t)\) continue en entrée se transforme en
impulsions quasi-sinusoïdale en sortie du chopper (disque avec des trous qui tourne). La fréquence,
taille et forme de ces impulsions dépendent de la géométrie du chopper ainsi que de sa vitesse de
rotation.
Le champ électrique \(E(t)\) passe donc d’une forme sinusoïdale à une forme plus complexe où
on peut distinguer 2 périodes au lieu d’une : une oscillation rapide correspondant à la période du
champ électrique du signal d’origine, et une oscillation lente correspondant au nombre de fois que
le chopper est passant par seconde (sur l’exemple, si le chopper fait 1 tour par seconde il sera
passant toutes les 0, 5 secondes).
Il existe un autre phénomène qui créer aussi un champ complexe tel que celui présenté ici qui
est l’interférence entre deux champ électrique de période légèrement différentes (Fig.3) :
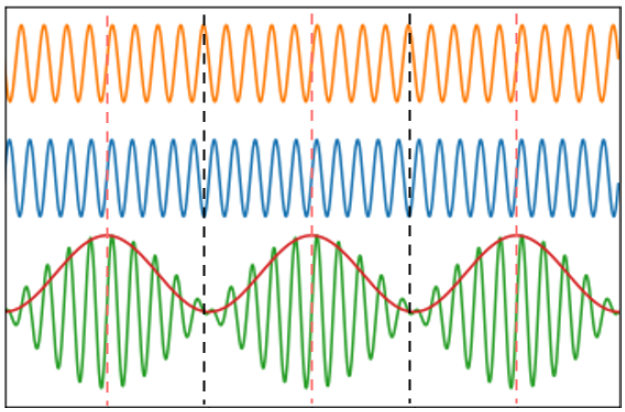
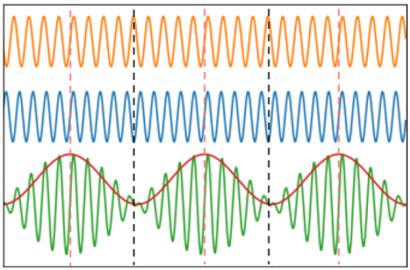
Figure 3 – Schéma de l’interférence entre deux champs électrique de périodes légèrement
différentes (0,1 Hz de différence). Orange et bleu : deux champs électrique, de fréquence \(f_1\) et
\(f_2\), qui vont interférer ensemble. Vert : champ résultant de l’interférence des deux champs. Rouge : Enveloppe du champ résultant (impulsion). Pointillé rouge : interférence constructive. Pointillé
noir : interférence destructive.
Dans ce cas, les deux périodes rapide et lente sont :
\[ T_{lent}=\frac{2}{f_1+f_2} \] \[ T_{rapide}=\frac{1}{|f_1-f_2|} \]
Avec \(T\) les périodes temporelles et \(f_1\), \(f_2\) les fréquences des deux champs interférents.
Quand on se rapproche de l’interférence constructive l’amplitude du champ résultant augmente
(pointillé noir vers pointillé rouge), et quand on se rapproche de l’interférence destructive l’amplitude
du champ diminue (pointillé rouge vers pointillé noir). Cela résulte donc en une enveloppe et
un champ électrique avec les mêmes propriétés que celle du faisceau découpé par le chopper.
Comme les deux phénomènes sont analogues, on peut expliquer la création du champ complexe
en sortie du chopper par la création de deux nouveaux champs électrique de fréquence \(f_1\)
et \(f_2\) qui interfèrent entre eux. Cette manière de décomposer un signal périodique avec une structure complexe en somme de signaux sinusoïdaux est appelée une décomposition de Fourier ou une transformée de Fourier discrète. On peut donc représenter tous les signaux périodiques par une
superposition de signaux sinusoïdaux de périodes différentes. Cela revient à décomposer le signal
en ses composantes spectrales (différentes périodes), avec l’intensité de ces composantes proportionnelle à l’amplitude des sinusoïdes décomposées = si on affiche les intensités en fonction de la longueur d’onde/fréquence, on obtient le spectre de notre signal (d’où la transformée de Fourier, on passe du domaine temporel au domaine fréquentiel que l’on peut convertir en nm avec \(\nu= c/\lambda\)).
Dans les exemples précédents on a fait interférer 2 champs, mais on peut en faire interférer
autant qu’on veut. La conséquence est que l’on va créer des zones où le champ électrique résultant
non nul seront plus petites, et donc au niveau de l’enveloppe (éclairement) on aura des successions
d’impulsions de plus en plus petites et rapprochées au fur et à mesure que l’on ajoute des champs
électrique de périodes différentes.
Ce principe est celui des lasers impulsionnels, c’est en ayant une très grande quantité de champs
électrique avec des périodes différentes que l’on peut avoir des impulsions lumineuses, dont les plus
courtes obtenu au moment de la rédaction atteignent 43 attoseconde [2] (\(43 \times 10^{−18}\) seconde).
Ainsi, on vient d’expliquer ce qu’était la lumière, ses propriétés en tant qu’onde, la relation
entre le domaine temporel et fréquentiel (Transformée de Fourier), que des impulsions lumineuses
sont le résultat de l’interférence entre plusieurs champs électrique que se soit par l’addition de ces
champs ou par la découpe spatiale d’un champ continue.
Conclusion
Pour finir, toute cette explication été faite en ne prenant pas en compte la cohérence des
champs électromagnétique. Car les phénomènes décrit plus haut ne sont possibles que si les champs
sont cohérents entres eux, c’est-à-dire si ils se propagent dans la même direction et avec la même
phase, ce qui n’est pas le cas pour la lumière naturelle et donc pourquoi, par exemple, le soleil
ou les lampes blanches n’envoient pas d’impulsions alors qu’ils émettent dans toute la gamme du
visible en même temps.
Je trouve que ce type d’approche plus intuitive manque dans les formations de physique, comme il y énormément de théorie à apprendre ce côté n’est pas approfondi. La thèse m’a permis de beaucoup améliorer mon intuition physique pour mieux comprendre les phénomènes avec lesquels je travaille comme avec l’exemple de ce texte qui permet de comprendre comment fonctionne la modulation de champ électrique et donc, pour ma thèse, me permet de bien mieux comprendre
comment fonctionne les lasers électro-optique qui sont des lasers avec une très haute cadence de tir (dizaines de milliard d’impulsions par seconde) contrôlé/modulé électroniquement.
Références
[1] https ://theory.labster.com
[2] Thomas Gaumnitz, Arohi Jain, Yoann Pertot, Martin Huppert, Inga Jordan, Fernando Ardana-
Lamas, and Hans Jakob Wörner, ”Streaking of 43-attosecond soft-X-ray pulses generated by a
passively CEP-stable mid-infrared driver,” Opt. Express 25, 27506-27518 (2017)