C’est quoi une BSS ?
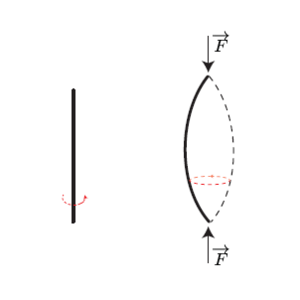
Une BSS a lieu lorsque l’état fondamental d’un système ne possède pas les symétries de son Hamiltonien. En mécanique classique il existe de nombreux exemples de BSS, par exemple le flambage d’une poutre[1] sur laquelle on exerce une force de compression. Malgré la symétrie de rotation autour de son axe principal, la poutre va spontanément prendre une courbure dans une certaine direction. Tous les états fondamentaux (les différentes orientations de la poutre) sont dégénérés en énergie (Fig. 1).
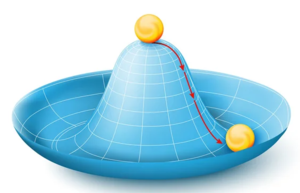
On peut également citer une balle sur le sommet d’une colline, ou comme sur la Fig. 2, au sommet d’un chapeau mexicain. La moindre perturbation va entraîner la balle vers un endroit spécifique au fond du puits de potentiel formé par le chapeau. Tous les états fondamentaux sont encore une fois reliés par une rotation autour de l’axe du chapeau.
En mécanique quantique les aimants sont également des exemples fameux de BSS. L’Hamiltonien du modèle d’Heisenberg des ferromagnétiques est invariant suivant la rotation globale des spins. Cependant, sous la température de Curie, la magnétisation devient <m> ≠ 0 ; les spins vont spontanément briser la symétrie en choisissant une orientation privilégiée.
Le cas de la chaise
On peut considérer qu’une chaise est décrite par l’Hamiltonien général suivant :
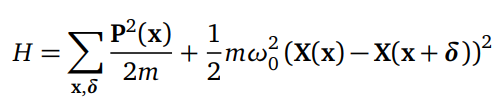
Ce dernier commute avec la quantité de mouvement totale. Les états propres sont donc états propres de l’impulsion, donc non-localisés dans l’espace. Il est possible de montrer que les états propres décrivant la dynamique du centre de masse ont une énergie ~ (Ptot)²/N, avec Ptot l’impulsion totale et N le nombre d’atomes dans le cristal. On a donc une échelle d’énergie espacée de façon inversement proportionnelle à la taille du système. Pour un système infini, les états propres de l’impulsion sont donc dégénérés et le système peut, sans coût énergétique, avoir une localisation dans l’espace. Les systèmes réels sont cependant finis. Rajoutons une perturbation à l’Hamiltonien :
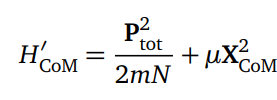
Cette dernière tend à localiser les atomes à l’origine des coordonnées. On reconnaît un oscillateur harmonique ; l’état fondamental est alors donné par une gaussienne centrée en 0. En prenant la limite N → ∞, µ →0 (dans cet ordre), on obtient un pic de Dirac en 0, donc une localisation de l’état fondamental en 0. En prenant l’ordre inverse des limites on obtient à nouveau un système non-localisé. La limite thermodynamique est donc singulière, comme dans le cas du modèle d’Ising ferromagnétique : c’est le signe typique d’une BSS. Maintenant, on peut se demander quelle perturbation permet d’avoir une chaise bien localisée, disons à un centième de la taille d’une maille élémentaire (~ 10-12m). On trouve qu’il faut prendre une perturbation µ de 1 zeptonewtons (10-21N) par centimètre. De telles forces sont à la limite des techniques expérimentales actuelles. Il est donc en pratique impossible de trouver une chaise dans un état propre de l’impulsion.
Mécanisme de Higgs, BSS et supraconductivité
Le mécanisme de Higgs a lieu lorsqu’une symétrie de jauge est spontanément brisée. Le cas le plus connu est celui de la brisure spontanée de la symétrie de jauge SU(2)×U(1) de l’interaction faible qui permet, via le mécanisme de Higgs, aux 3 des 4 vecteurs de jauge de la théorie d’acquérir une masse : ce sont les bosons W±, Z0. Elle explique également l’origine de la masse des fermions (hors neutrinos). Mais ce mécanisme est également présent dans des systèmes à beaucoup plus basse énergie. Le cas le plus fameux est celui de la supraconductivité. Toutes les propriétés des supraconducteurs peuvent être expliquées en terme de BSS. Lorsqu’un métal passe de l’état normal à l’état supra, la symétrie de jauge U(1) de l’électromagnétisme est brisée ; la conservation de la charge est alors en apparence violée et le photon acquiert une masse. Sans entrer dans les détails, ceci permet d’expliquer l’effet Meissner (le fait qu’un supraconducteur expulse tout champ magnétique), la résistance au courant nulle, …
Conclusion
Le concept de brisure spontanée de symétrie est un concept général qui permet de décrire énormément de phénomènes physiques, du flambage d’une poutre à l’origine de la masse des particules élémentaires.
Références :
[1] Weinberg, S. (1996) The Quantum Theory of Fields Vol. 2, Cambridge University Press.
[2] Beekman et al., An introduction to spontaneous symmetry breaking, SciPost Phys. Lect. Notes
[1]Le flambage est un phénomène d’instabilité d'une structure élastique qui pour échapper à une charge importante exploite un mode de déformation non sollicité, opposant moins de raideur à la charge. Par exemple dans le cas d’une règle en plastique, si ses extrémités sont tenues et comprimées dans le sens de la longueur, la règle va se plier et se briser avec un effort de compression bien plus faible que celui nécessaire à la rupture en traction (Wikipédia).

C’est quoi une BSS ?
Une BSS a lieu lorsque l’état fondamental d’un système ne possède pas les symétries de son Hamiltonien. En mécanique classique il existe de nombreux exemples de BSS, par exemple le flambage d’une poutre[1] sur laquelle on exerce une force de compression. Malgré la symétrie de rotation autour de son axe principal, la poutre va spontanément prendre une courbure dans une certaine direction. Tous les états fondamentaux (les différentes orientations de la poutre) sont dégénérés en énergie (Fig. 1).