Réseaux de contacts et comment voir que les hommes mentent
Aujourd’hui on va voir ensemble ce qu’est un réseau sans échelle (scale free en anglais) et quelles sont ses applications et ses implications dans la vie quotidienne. On verra aussi comment cela s’applique aux épidémies (même si, je le sais, vous en avez marre !), en particulier comment identifier les meilleures modalités pour une vaccination efficace.
Donc, imaginez un réseau qui a peu (mais pas zéro !) de nœuds avec beaucoup de connections sortantes et beaucoup de nœuds qui ont très peu de connections sortantes (de l’ordre de quelques-unes). C’est un réseau sans échelle, car un nœud quelconque n’a pas de nombre typique de connections que nous pouvons essayer de deviner à l’avance. La distribution des connections est, pour ces réseaux, une loi de puissance. Beaucoup de réseaux réels se comportent de cette façon-là, comme le web, les connections aéroportuaires, Facebook, ou encore le réseau de contacts sexuels humains (cf. Fig. ci-après). Les scientifiques pensent que la raison pour laquelle ce type de réseau se forme dans la nature, ou dans les créations humaines, est le mécanisme d’attachement préférentiel.
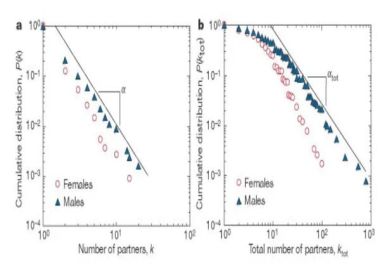
Figure 1 Adapté par Liljeros, Fredrik, et al. "The web of human sexual contacts." Nature 411.6840 (2001): 907-908.
Donc pour expliquer comment il fonctionne, imaginez quelqu’un qui est obèse, et bien, selon ce mécanisme, cette personne a plus de chance de grossir encore, et devenir ainsi très obèse, qu’une personne maigre ou en poids normal. Mais étant donné que les personnes obèses sont une minorité, à la fin on aura très peu de personnes très obèses, peu de personnes obèses et beaucoup de personnes maigres ou en poids normal. En rapportant cela aux réseaux, c’est ce qu’il se passe.
Regardons maintenant la figure ci-dessus, il s’agit donc de la distribution cumulative du nombre de partenaires sexuels pour les hommes (triangles) et pour les femmes (ronds) (à gauche dans les derniers 12 mois, à droite sur toute la vie). On peut voir que la distribution est fortement semblable à une distribution en loi de puissance (une droite dans un plot log-log comme sur la figure). Ce qui est drôle c’est que la moyenne de partenaires sexuels est plus grande pour les hommes que pour les femmes, alors qu’étant donné que la population est homogène et hétérosexuelle, évidemment on s’attend à ce qu’en moyenne les femmes ont eu des actes sexuels avec les hommes autant que les hommes avec les femmes. En plus, comme la pente de la droite α est identique, dans les erreurs statistiques (au tour de 2.3), on peut conclure que les hommes mentent, eh oui nous gonflons le nombre de partenaires (en fait il est aussi possible que les femmes le baissent, mais bon je ne pense pas !).
Dans tous les cas, une fois qu’on a vu que le réseau de contacts est un réseau sans échelle, on peut se demander par exemple quelles implications cela peut avoir dans la diffusion de maladies, sexuelles en l’occurrence. On peut prouver que dans ce type de réseau il existe un seuil critique de transmissibilité de la maladie (la probabilité de la transmettre à un de nos contacts) au-delà duquel la maladie devient une épidémie, elle touche donc une fraction importante de la population. Ce seuil critique dépend de la pente de la loi de puissance propre du réseau (cf. figure).
Figure 2 Adapté par Newman, Mark EJ. "Spread of epidemic disease on networks." Physical review E 66.1 (2002): 016128.
Il est très intéressant de voir que pour un α plus petit de 2 le seuil est à zéro (mauvaise nouvelle !), et donc aucune politique de limitation de la maladie ne pourra aider : l’épidémie explosera de toute manière. Au contraire, si α est plus grand que 2.48 la maladie s’arrêtera toute seule (très bonne nouvelle !). Cependant si l’exposant est entre les deux on peut activement faire quelque chose pour arrêter la maladie, la réalité nous dit que α est effectivement dans cet intervalle (comme par miracle !). Que peut-on donc faire dans le cas réel pour pouvoir arrêter la transmission de ces maladie sexuelles ? En fait, il suffirait simplement de limiter (physiquement ou par vaccination, si possible) les contacts de 1.3 % de la population qui a le plus d’activité sexuelles, et donc il n’y a pas du tout besoin d’agir sur tout le monde !
Stefano Polizzi
Auteur
Stefano Polizzi, Doctorant au LOMA
