Le principe de Fermat et électrodynamique quantique

Il y a quelques années, n’étant encore qu'un jeune physicien en première année de licence, j'ai été confronté en cours d'optique géométrique au principe de Fermat. En thèse, j'ai été assez surpris de trouver une explication dans des livres d'électrodynamique quantique.

Le principe de Fermat stipule que sur tous les trajets possibles permettant de relier deux points dans l'espace, la lumière suivra toujours celui qui minimise son temps de trajet.

Ce principe m'avait à l'époque interpellé car j'avais l'impression que l’on donnait des intentions conscientes à la lumière. Comment peut-elle savoir quel est le trajet le plus court en temps ? Comment décide-t-elle de suivre ce chemin plutôt qu'un autre ?

Toutefois, si on considère des rayons lumineux, ce principe permet de retrouver un bon nombre de lois remarquables, comme le fait que la lumière se propage en ligne droite, et que le rayon se "brise" lors du passage dans un autre milieu (loi de réfraction, dite des sinus) ; ceci expliquant finalement le fonctionnement des miroirs, lentilles optiques ou mirages. Si on accepte ce principe étrange, tout semble assez bien fonctionner (si on oublie les phénomènes purement ondulatoires).

À mon arrivée en thèse, j'ai été assez surpris de trouver une explication de l'efficacité de ce principe dans des livres d'électrodynamique quantique, à savoir la théorie quantique de la lumière.

La physique quantique explique en substance qu'on ne peut pas prédire l'état d'une particule tant qu'on ne l'a pas mesuré, et que tant que cet état n’est pas connu, tout se passe comme si toutes les configurations possibles étaient effectivement réalisées (principe de superposition).

Le plus étrange étant que ces configurations peuvent interférer entre elles : si on considère deux chemins possibles pour qu'une particule passe du point S au point D, avec une probabilité p associée à chacun des chemins, la probabilité finale de trouver une particule en D (sachant qu'elle est partie de S) peut osciller entre 2p et 0 alors qu'on s'attendrait classiquement à toujours avoir une probabilité 2p quelque soit la configuration expérimentale !

Ces règles d'interférences sont connues, et peuvent être comprises géométriquement : si deux chemins ont des distances de parcours proches, la probabilité finale sera supérieure à p (interférences constructives), alors que si les distances de parcours sont (suffisamment mais pas trop) éloignées, la probabilité sera plus faible (interférences destructives). La probabilité finale pour qu'une particule partant de S soit retrouvée en D dépend donc de la différence de distances entre ces trajets (techniquement de leurs différences de phases), et ceci en prenant en compte tous les trajets possibles !

Bien que les principes de la physique quantique ne soient pas moins choquants pour l'intuition que le principe de Fermat, ils permettent d'expliquer avec une étonnante précision tous les phénomènes connus faisant intervenir la lumière et la matière, dont les liaisons atomiques et chimiques, les réseaux optiques, et tout un tas de processus plus amusants les uns que les autres (si on aime le calcul).

Dans ce cadre théorique (qui est le cadre de la physique actuelle), le principe de Fermat s'explique comme suit :

La lumière peut suivre tous les chemins entre les points S et D, avec une probabilité p associée à chaque chemin
Pour un chemin donné, on regarde l'influence des autres chemins sur la probabilité finale : si les distances parcourues sont proches, la probabilité finale de trouver la particule en D augmente, sinon elle diminue
Géométriquement, les distances de parcours sont très similaires sur les trajets proches du temps minimal, et très différentes sur les autres trajets
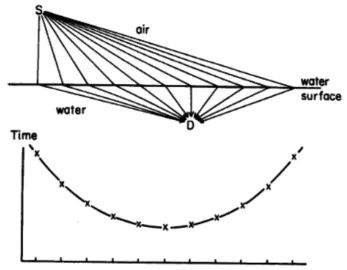
Il s'ensuit que la zone qui contribue le plus à la probabilité finale est au voisinage du chemin le plus court en temps (voir figure)

Si on regarde de suffisamment loin, il nous semble donc que la lumière passe par un trajet unique, qui correspond au temps de trajet minimal, car les autres possibilités sont très peu probables. Le principe de Fermat est alors une conséquence aux grandes distances de la nature quantique de la lumière !

Fermat ne pouvait bien entendu pas deviner cela, mais je trouve toujours magnifique la façon dont les développements théoriques de la physique amènent à démontrer des principes anciens (après 3 siècles de travail, du XVIIème aux années 1960), et ceci en se basant sur une compréhension plus profonde de ce que semble être la logique de notre univers.

Pour aller plus loin sur ce sujet, je recommande vivement la lecture du livre de Richard Feynman : Lumière et Matière .

Léo Esnault

Mise à jour le 08/03/2019