Introduction aux systèmes frustrés

Beaucoup de matériaux suivent ce type de processus : une phase gazeuse à haute température
où les particules (comme les molécules d’eau) ne se voient pas et sont décorrélés. Une phase liquide où les particules s’agencent avec leurs voisins proches mais ne forment pas une structure cohérente avec des particules lointaines, ils sont corrélés à courtes distances mais décorrélés à longue distance. Puis une phase solide à basse température où les particules s’agencent fortement entre eux et, de proche en proche, créent une structure ordonnée même avec les particules lointaines, ils sont corrélés à longue distance.

On s’intéresse maintenant aux matériaux magnétiques qui sont formés d’un arrangement régulier d’atomes où on peut chacun leur associer un petit aimant, qu’on va appeler un spin. Si les spin s’alignent sur un axe, ils peuvent prendre deux valeurs : "up" (aligné nord-sud) ou "down"
(aligné sud-nord). Si les spin interagissent entre eux de manière à favoriser un alignement entre spins voisins, à haute température on aura une phase décorrélée où tous les spins seront aléatoirement up ou down (paramagnétique), et à basse température on aura une phase corrélée à longue distance où tous les spins sont alignés (ferromagnétique), créant un aimant global comme ceux que vous pouvez retrouver sur votre frigo. Ceci correspond bien au comportement habituel avec la température, même si on saute la phase liquide et on passe directement du gaz au solide. Cependant, si les spins interagissent de manière à s’anti-aligner entre voisins, certains arrangements d’atomes, comme le triangle, ne permettent pas à chaque voisin de s’anti-aligner, le système est alors frustré ; le meilleur arrangement pour chaque spin, où tous ses voisins s’anti-alignent, n’est pas compatible avec le système global. Ceci fait que chaque triangle a beaucoup d’arrangements où 2 paires de voisins sont anti-alignés et 1 paire de voisins sont alignés. Donc à haute température on a toujours une phase décorrélé, mais en baissant la température on tend vers une phase où chaque triangle est frustré et il existe une infinité de manières d’arranger les spins pour le système global. On perd alors la corrélation longue distance tout en gardant des corrélations à courte distance, on se trouve alors plutôt dans une phase liquide, même à très basse température, au lieu d’aller vers une phase solide. La frustration a empêché l’ordre de se former.

Ceci était un exemple de frustration dans un monde classique mais souvent, dans les matériaux, les interactions entre les spins seront de nature quantique. Le lecteur intéressé pourra se référer au Chapitre 2 de "An introduction to Quantum spin models" pour une description plus détaillé, mais pour l’instant on peut dire qu’on autorise la solution à être une superposition d’arrangements classiques (une somme pondéré des arrangements), et que cette interaction quantique tend de nouveau à anti-aligner les spins mais contient aussi un terme qui stabilise les solutions qui contiennent une superposition d’états où les spins voisins ont été échangés, qu’on nomme le terme d’échange. Si on prend 2 spins en interaction, on forme alors un singulet, une superposition des deux états antialignés. En passant sur triangle, le singulet sur un des cotés du triangle reste la solution. On peut continuer ceci en agençant plusieurs triangles ensemble, on peut assigner un singulet à chacun d’entre eux, mais si on voulait fermer les boucle pour définir un réseaux 2D, il y aurait un encombrement entre les singulets et il faut alors trouver une autre solution.

Malheureusement, puisque notre solution peut être une superposition de tous les états classiques, alors pour trouver une solution à un système avec N spins en interaction, il y a 2^N arrangements classiques, et il faut diagonaliser une matrice de dimension 2^N. Pour l’instant, les tailles de systèmes qui sont accessibles par cette méthode sont autour de 40 spins, ce qui demande déjà de diagonaliser
une matrice de plus de mille milliards de dimensions.

Un état quantique dans un réseau de neurones

Une façon de pallier à ce problème est d’observer que toute solution quantique sera une superposition d’états classiques, donc il faut trouver les coefficients de la somme pondéré, mais au lieu de directement trouver les 2^N coefficients, on peut essayer de trouver une fonction, qu’on
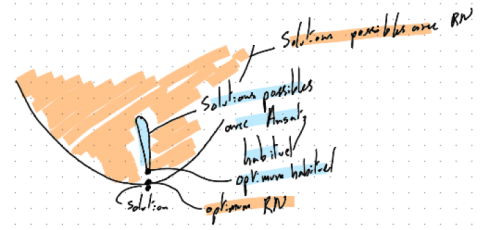
nomme une Ansatz, qui prend une configuration classique en entrée et donne son coefficient en sortie. On peut alors garder toute l’information sur la solution dans l’Ansatz plutôt que de stocker en mémoire les 2^N coefficients.

Souvent cette Ansatz sera déterminé grâce à raisonnement physique et sera paramétrisé avec une dizaine de paramètres. On sait que la solution sera la fonction d’onde avec l’énergie la plus basse, on peut alors jouer avec avec les paramètres pour trouver l’Ansatz de plus basse énergie de façon à se rapprocher de la solution. Puisque le nombre de paramètres est petit, le nombre de solutions accessibles n’est pas grand, on peut dire que l’Ansatz n’est pas très expressif, mais la forme de l’Ansatz
découle d’un raisonnement physique propre au système donc il est souvent bien adapté au problème. Cependant, il existe des cas où on ne peut pas trouver un raisonnement qui convient à notre système et on à besoin d’un autre moyen pour trouver la solution, on peut alors employer la puissance de calcul des réseaux de neurones.

Le domaine de l’apprentissage machine à vu des développements fulgurants récemment qui ont conduit au déploiement des modèles génératives de texte ou d’images, et à du progrès scientifique sur le repliement des protéines ou des découvertes d’algorithmes plus efficaces pour les multiplications de matrices. Ces progrès sont en grande partie dues au développement des réseaux de neurones, le lecteur intéressé pourra trouver une introduction à ces modèles ici. On va se contenter ici de dire qu’ils sont composés d’une entrée (comme la configuration de spins classiques),
auquel on applique un succession de transformations linéaires et non-linéaires jusqu’à arriver à une sortie (comme le coefficient associé à la configuration de spins classiques). En somme, cela nous donne une grande fonction non-linéaire qui peut associer les configurations de spins à leurs coefficients. Les réseaux de neurones ont typiquement plusieurs centaines de milliers de paramètres,
ceci les rend très expressives. Même si ils ne sont pas conçus spécifiquement pour un système en particulier, leur énorme expressivité leur permet d’approcher très fortement la vraie solution. De plus, il existe un théorème démontrant que, si on avait un réseau de taille infini on pourrait approximer toutes fonctions continues, donc en augmentant la taille du réseaux on peut s’approcher de plus en plus vers la vraie fonction d’onde.

Cependant, même si un tel Ansatz devrait converger vers la bonne solution, il y a toujours un problème puisque ceci n’est seulement vrai que dans la limite de l’infinité de neurones, mais vu que nous en avons une nombre limité, et un temps limité pour l’apprentissage, on ne peut que bien
approximer les solutions de certains systèmes. L’effort aujourd’hui est alors de développer des architectures de réseaux de neurones qui arrivent à trouver des solutions pour des systèmes très variés. C’est une approche qui est, malgré son développement récent, déjà à la pointe de la recherche et est compétitif avec, voir surpasse d’autres méthodes similaires.