Rhéologie des cellules vivantes et dérivation fractionnaire

La cellule est le constituant élémentaire des organismes vivants. C'est un système incroyablement complexe à décrire par des modèles physiques qui ne parviennent à en dépeindre que certains aspects très spécifiques. L'un d'eux est sa réponse en tant que matériau à une excitation mécanique, qu'on appelle la rhéologie. Il existe aujourd'hui plusieurs techniques de micromanipulation pour venir titiller une cellule isolée (quelques µm à centaines de µm) et étudier sa relaxation telles que le levier du microscope à force atomique (AFM).
Les comportements rhéologiques basiques des systèmes inertes sont décrits par des équations très simples : un matériau élastique, comme un ressort ou la plupart des solides, va se déformer proportionnellement à la force (ou contrainte) exercée sur lui. Réciproquement, en réaction à une déformation x(t), il va s'y opposer avec une force proportionnelle f(t) = kx(t). Le coefficient de proportionnalité k est sa raideur. En revanche, dans le cas des matériaux visqueux (les liquides), la force de réaction n'est plus proportionnelle à la déformation exercée, mais à sa dérivée par rapport au temps : f(t) = ηx’(t) et le coefficient de proportionnalité η décrit la viscosité.
Lorsqu'ils sont combinés en série ou en parallèle, ces composants mécaniques élémentaires peuvent décrire des rhéologies différentes à petites et grandes échelles de temps. Ce type de modèle viscoélastique n'est pas approprié pour décrire la rhéologie des cellules, qui nécessiterait un nombre infini de composants pour la reproduire. Il existe une relation mathématique synthétique pour décrire cela : la dérivée fractionnaire, f(t) = G0x(α)(t) où l'ordre de la dérivée α est d’ordinaire un entier positif. Il est cependant possible de définir la dérivée fractionnaire pour tout ordre réel et la viscoélasticité des cellules a un ordre α compris entre 0 (cas élastique) et 1 (cas visqueux). Le domaine fréquentiel est la manière la plus facile de l'appréhender, c'est-à-dire grâce à la transformée de Fourier qui permet de décomposer la dynamique en oscillations d'amplitudes et de fréquences différentes : F(ω)=G(ω)X(ω). On a simplement G(ω) = k dans le cas élastique, (iω)η dans le cas visqueux et (iω)αG₀ dans le cas fractionnairement viscoélastique. Les composantes oscillatoires de fréquence ω sont alors déphasées de α quart de période et amplifiées d’un facteur ωα entre l'excitation et la réponse. C'est ce dernier point qui est représenté dans le graphique ci-après.
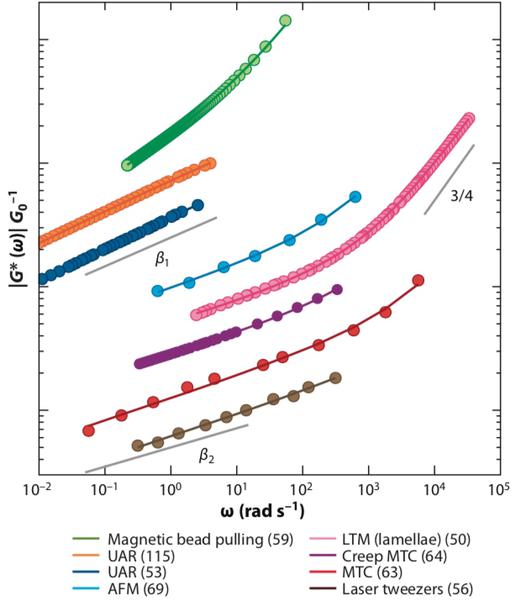
Les données collectées sur des cellules vivantes avec des techniques différentes mettent en évidence une très nette loi de puissance |G(ω)|~ωα où α ≈ 0,25 pour une grande diversité de cellules. Cette invariance d'échelle témoigne d'une architecture complexe et multi-échelles (réseaux de filaments protéiques constituant le cytosquelette). Cette facette de la vie cellulaire est maintenant claire : une cellule unique, eucaryote et adhérente, répond lorsqu'on la stimule en exerçant environ « un quart de dérivée » de la sollicitation. Mais on aperçoit déjà les limites de ce modèle à hautes fréquences (cf. graphique), et l'on se doute qu'à des temps de l'ordre d'une division cellulaire (très basses fréquences inaccessibles ici), le comportement mécanique est autrement plus complexe : alternant entre périodes plus élastiques que visqueuses entre deux divisions cellulaires et périodes plus visqueuses qu'élastiques au moment de la division cellulaire.
Le mystère est encore grand en physique des systèmes vivants !
Pour en savoir plus à ce sujet :
1. Chalut, Paluch, 2016. The actin cortex: a bridge between cell shape and function. Developmental Cell 38
2. Gallet et al., 2009. Power spectrum of out-of-equilibrium forces in living cells. Soft Matter 5
3. Gerasimova-Chechkina et al., 2018. Fractional rheology of muscle precursor cells. Journal of Rheology 62
4. Hoffman, Crocker, 2009. Cell mechanics: dissecting the physical responses of cells to force. Annual Review of Biomedical Engineering 11
Auteur
Alexandre Guillet, Doctorant au LOMA













